第三章 线性方程组:这一章的中心问题是讨论线性方程组的解的基本理论,即非齐次线性方程组有解和齐次线性方程组有非零解的充分必要条件以及它们解的结构。为了求非齐次线性方程组的通解,必须能求得齐次线性方程组的通解,具体说需要求得其方程组的一个基础解系。由于基础解系是一组线性无关的解向量组成,这样判断向量组是线性无关是必须的。同时,在判定非齐次线性方程组是否有解,还需要学习矩阵的秩。3.1线性方程组:一个向量组的线性组合。一个向量可由一向量组线性表示;一个向量组的线性组合等于零向量,若他们的系数不全为零,则该向量组线性相关。否则,该向量组线性无关。 判定向量组线性相关和线性无关,可以通过假设有一组常数使得向量组的线性组合等于零向量,当求得这组常数不全为零,则向量组线性相关;当求得这组常数全为零,则向量组线性无关。[单选题]
3.2向量组的秩及其极大线性无关组:一向量组A的任意向量可由一向量组B线性表示,则称向量组A可由向量组B线性表示;若向量组B也可由向量组A线性表示,则称向量组A与向量组B等价;两个向量组等价,秩相等;向量组A可由向量组B线性表示,向量组A所含向量的个数大于向量组B所含向量的个数,则向量组A线性相关。
3.3矩阵的秩和相抵标准型:矩阵的行秩等于列秩;初等变换不改变矩阵的秩;矩阵的秩等于矩阵的行秩和列秩;矩阵的秩等于该矩阵经过初等行变换得到的阶梯型矩阵的非零行的行数;矩阵的性质;满秩矩阵是非奇异矩阵,是可逆矩阵。
3.4齐次线性方程组有非零解的条件及解的结构.:齐次线性方程组的系数矩阵,通过行变换,将其化为简化阶梯型矩阵,确定矩阵的秩,选择基础未知量和自由未知量,求得齐次线性方程组的基础解系,最后求得该方程组的通解。
3.5非齐次线性方程组有解的条件及解的结构:对于非齐次线性方程组,首先判定方程组是否有解;理解有解的条件,即增广矩阵的秩等于系数矩阵的列数;其次,当方程组有解时,增广矩阵的秩等于系数矩阵的列数,方程组有唯一解;小于系数矩阵的列数时,有无穷多解;求其一个特解,再求其对应的齐次线性方程组的通解。
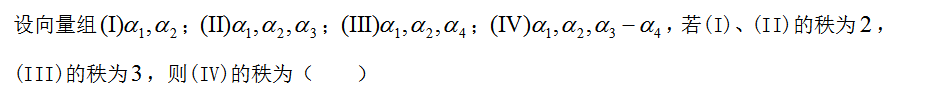 选项:[4, 1, 3, 2]
选项:[4, 1, 3, 2] [单选题]
 选项:[
选项:[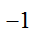 ,
, 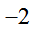 ,
, 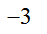 ,
, 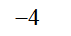 ]
][单选题]
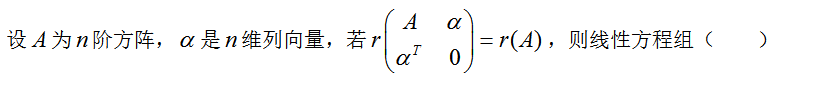 选项:[
选项:[ ,
, 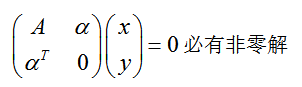 ,
, 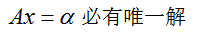 ,
, 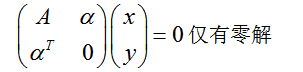 ]
][单选题]
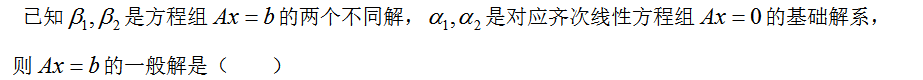 选项:[
选项:[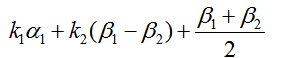 ,
, 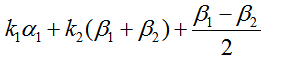 ,
, 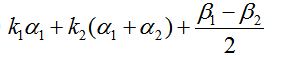 ,
, 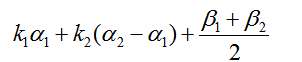 ]
][单选题]
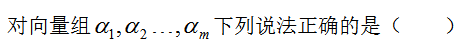 选项:[
选项:[ ,
, 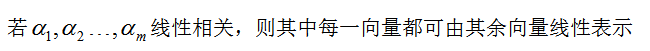 ,
,  ,
,  ]
]
温馨提示支付 ¥1.00 元后可查看付费内容,请先翻页预览!

