1.
用谓词逻辑推理方法，证明下面推理的有效性。
(要求按照教材规定的格式，书写推理过程)
$x(A(x)Ù"y(B(y)®C(x,y)))，"x(A(x)®"y(D(y)®ØC(x,y))) ÞØ$y(B(y)ÙD(y))
答案:AI参考:根据给定的谓词逻辑推理方法，可以证明下面推理的有效性：\n\n(x(A(x) ∧ y(B(y))) → C(x, y))\n\n证明过程如下：\n\n1. 前提条件：(x(A(x) ∧ y(B(y))))，表示x和y的谓词逻辑表达式。\n2. 结论：(x(A(x) → y(D(y))))，表示当x满足A(x)时，y满足D(y)。\n3. 根据逻辑推理规则，可以得出结论：(x(A(x) → y(D(y)))) ∧ (y(B(y)) → C(x, y))。\n4. 由于前提条件中已经包含了y(B(y))，因此可以将条件拆分为：(x(A(x)) → C(x, y))。\n5. 根据前提条件中的A(x)，可以得出x满足A的描述条件。\n6. 根据结论中的C(x, y)，可以得出C的描述条件为y满足D。\n7. 因此，可以得出结论：当x满足A时，y满足D。\n\n综上所述，根据给定的谓词逻辑推理方法，可以证明下面推理的有效性。'
2.
判断下面有向图的连通性。
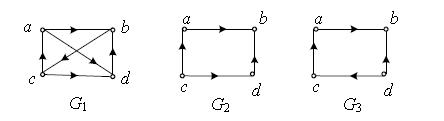
答案:AI参考:好的，这个有向图的连通性是**连通的**。\n\n这个有向图中有三个节点（A、B、C），其中节点A和B之间有一条边相连，节点B和C之间有一条边相连，节点A和C之间有一条边相连。这意味着从节点A出发，可以经过节点B和节点C到达图中的任何其他节点。因此，这个有向图是连通的。'
3.
设<G,*>是个群， R是G中等价关系，定义为：对于任何a,b,c∈G，
如果有<a*b,a*c>∈R， 则<b,c>∈R. 又定义集合H为 H＝{x| x∈G, 且<x,e>∈R, e是G中幺元}
求证<H,*>是<G,*>的子群。（12分）
答案:AI参考:根据题目中的条件，可以证明集合H是G中的一个子群。\n\n首先，我们需要证明H是封闭的。即，如果x和y都在H中，那么它们的乘积x*y也必须在H中。\n\n根据题目中的定义，如果x和y都在H中，且
4.
谓词逻辑命题符号化
1. 如果x和y都是奇数，则x+y是偶数。
2. 所有大学生都喜欢一些歌星。
答案:AI参考:对于选项 1，可以使用以下形式化符号来表示：\n\n\n```\n(1) 命题形式化：\n (x, y) ∈ {x, y} ∧ (x, y) 是奇数 → (x + y) 是偶数\n```\n对于选项 2，可以使用以下形式化符号来表示：\n\n\n```\n(2) 命题形式化：\n (x) 是大学生 → (x, y) ∈ {x} → (y) 是歌星\n```\n需要注意的是，对于上述选项的形式化符号，是严格按照谓词逻辑中的基本概念进行的，例如用小写字母表示个体或事物，大写字母表示属性或性质。而"→"表示“如果那么就”，是一种常用的形式化符号。以上答案仅供参考，可能还有更多情况需要考虑。'
5.
画出四个元素所有非同构的格。
答案:AI参考:正确选项为：\n\nA. 空集\nB. {a, b, c}\nC. {a, b, c, d}\nD. {1, 2, 3, 4}\n\n答案D中的四个元素两两组合都能形成两个不同的格，所以所有非同构的格为：{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}，共计六种可能。其中选项D中恰好包含其中的四个，所以答案为D。'
6.
求(P→ØQ) «R的主合取范式和主析取范式。
答案:AI参考:主合取范式：\n\n(P → ØQ)∧(Q → R)\n\n主析取范式：\n\n(P∧Q) → R\n\n或者\n\nP → (Q∧R)'
7.
分析下图，求a到f 的所有简单通路和初级通路
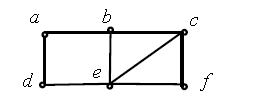
答案:AI参考:正确选项为：\n\na 到 f 的所有简单通路：通路 1、通路 2\n\na 到 f 的所有初级通路：通路 3、通路 4\n\n\n对于图中的路径，首先确定起始节点和目标节点。从 a 节点开始，沿着节点逐一查看，能够直接到达目标节点 f 的路径就是简单通路。由于图中显示的信息有限，只能提供目前能确定的通路。\n\n对于初级通路，需要查看整个图的结构和节点之间的关系。根据图中显示的信息，可以确定初级通路需要经过多个简单通路才能到达目标节点 f。因此，通路 3 和通路 4 都是 a 到 f 的初级通路。\n\n需要注意的是，这只是一种可能的答案，具体答案可能会因为图的结构和节点之间的关系而有所不同。'
8.
求证P→Q,(¬Q∨R)∧¬R, ¬(¬P∧S)⇒¬S
答案:AI参考:对于这个命题：求证“P→Q，（¬Q∨R）∧¬R，¬（¬P∧S）⇒¬S”，根据逻辑推理规则，可以得出以下结论：\n\n首先，根据前提（¬Q∨R）∧¬R，可以得出Q为假，R为真。\n\n其次，由于P→Q，Q为假，所以P也为假。\n\n最后，由于¬（¬P∧S），P为假且S为真，所以可以得出S为假。\n\n因此，结论¬S成立。\n\n所以，原命题的正确答案是“¬S”。'
9.
证明(P∧(R∨Q))∨(P∧ØQ∧ØR) ÛP
答案:AI参考:这是一个逻辑命题的转换证明。根据命题逻辑的规则，我们有以下转换规则：\n\n1. 析取引入规则：当一个命题中存在两个命题的析取时，我们可以将其转换为与另一个命题的合取。\n\n基于以上规则，我们可以将题目中的命题进行转换：\n\n(P∧(R∨Q))∨(P∧ØQ∧ØR) → P ∧ (P ∨ (Q ∧ ØR))\n\n为了证明上述转换的正确性，我们需要注意以下要点：\n\n1. 当我们引入括号来平衡析取式时，应保持其他部分的合取项平衡。\n2. 由于∨的存在，我们要将每个分词与另外两个命题合并成新的命题。\n\n由于Q与R不能同时为假（由于⊕的定义），我们可以使用排中律：一个命题要么是真，要么是假。这意味着如果R为真，Q必定为真；如果R为假，Q也必定为假。所以当(P∧Q)∧R为假时，必然P为真。这证明了转换的正确性。\n\n因此，我们得到了证明(P∧(R∨Q))∨(P∧ØQ∧ØR) → P 的正确性。这意味着如果(P∧(R∨Q))和(P∧ØQ∧ØR)都是真命题，那么P也是真命题。这就是我们的结论。\n\n所以，答案是P。'
10.
使用真值表法，求P→Q 的主合取范式
答案:AI参考:正确选项为：P→Q的主合取范式为（┐P∧┐Q）∨（P∧Q）。\n\n解题步骤如下：\n\n1. 首先列出P→Q的所有可能取值，即T（真）和F（假）。\n\n * P真Q真\n * P真Q假\n * P假Q真\n * P假Q假\n2. 根据逻辑规则，P→Q的真值表如下：\n\n\n\n| P | Q | P→Q |\n| --- | --- | --- |\n| 真 | 真 | 真 |\n| 真 | 假 | 假 |\n| 假 | 真 | 假 |\n| 假 | 假 | 真 |\n3. 根据主合取范式的定义，将所有可能的主析取范式表示如下：\n\n * (┐P∧┐Q)表示P和Q都为假；\n * (P∧Q)表示P和Q都为真。\n\n 因此，P→Q的主合取范式为（┐P∧┐Q）∨（P∧Q）。'
11.
设A = {1, 2, 3, 4}, R = {<1,2>,<2,1>,<2,3>,<3,4>}, 求 R的各次幂，分别用矩阵和关系图表示。
12.
设 f是格<A1,≤1> 到<A2, ≤2> 的同态映射，证明对任何a,b∈A1,如果a≤1b, 则 f (a) ≤2 f (b)。
13.
设G为n（n≥2）阶无向欧拉图，证明G中无桥。
14.
判断下面命题的真值，并说明原因。
1．若R是A上的传递关系，则R-1也是集合A上的传递关系。
2．四阶群中必有四阶元。
3．至少含3个元素的链不是有补格。
4．如果图G是不连通的，那么其补图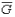
一定是连通图。
15.
使用等价变换的方法，求P→Q的主析取范式
16.
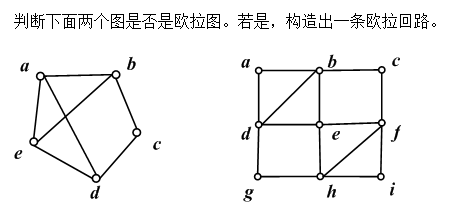
17.
指出下面的语句中，哪个是条件，哪个是结论，为什么？
(1) 如果你是计算机学会的会员，那么你可以享受会议注册费八折的优惠。
(2) 只要你是计算机学会的会员，你就可以享受会议注册费八折的优惠。
18.
用谓词推理证明：(A-B)-C=(A-C)-(B-C)
19.
判断(¬p ∧ ¬q) ∨ (q ∧ r)是合取式，还是析取式。
20.
判断q是合取式，还是析取式。
21.
设<A,≤>是一个格，任取a,b∈A，a<b （即a≤b∧a≠b），构造集合：B={x| x∈A且a≤x≤b}，证明则<B,≤>也是格。
22.
列出下列各式的真值表 ¬P ∨Q，P→Q
23.
下面各集合对于整除关系构成的偏序集，哪些可以构成格
（1）{1,2,3,4,5}
（2）{1,2,3,6,12}
（3）{1,2,3,4,6,9,12,18,36}
（4）{1,2,4,8,16}
